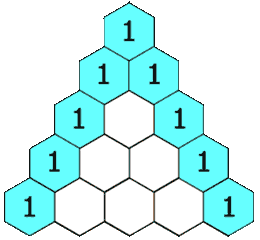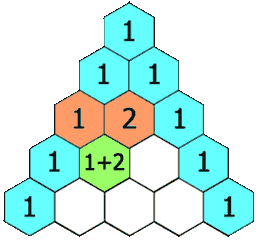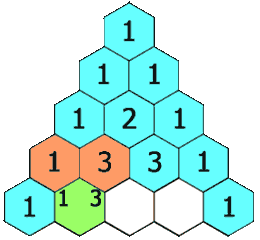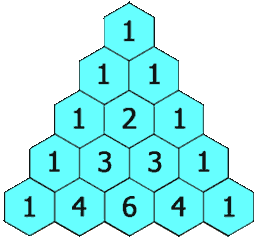
L’ingénieur et chercheur Jean-Claude Perez, Ph.D. a partagé avec moi l’une de ses études intitulée “De l’autre côté du miroir : le « sablier de Pérez », l’antimatière numérique du célèbre triangle de Pascal et les nombres de Fibonacci” (Through the Looking Glass: The “Perez Hourglass”, Digital Antimatter of the famous Pascal Triangle and Fibonacci numbers) que je m’empresse de partager avec vous. Chacun connait la suite de Fibonacci, clef de l’harmonie. Mais tous ignorent la “suite étendue de Fibonacci”, sorte de suite miroir ou palindrome, suite quasi symétrique de centre de symétrie le fameux ZERO, pivot de l’arithmétique séparant l’univers des nombres entiers positifs et entiers négatifs. Nombreux sont ceux aussi qui savent que la suite de Fibonacci est contenue et induite étrangement à partir du célèbre Triangle de Pascal. Mais tous ignorent qu’il existe une sorte de miroir du triangle de Pascal, symétrique avec comme pivot le nombre UN. Cet ensemble forme une sorte de sablier, nommé en 1997 le “sablier de Perez”, sablier duquel émergera… La “suite étendue de Fibonacci”, révélant ainsi une sorte d’antimatière numérique consistante et homogène du triangle de Pascal et de la suite de Fibonacci…

J’ai demandé au professeur Perez quelle serait la conséquence de cette découverte ? « Aucune idée… ». me répondit-il. « Mais mon intuition me dit que c’est important. » Il ajouta que le Dr Robert Friedman en obtint la confirmation par l’intermédiaire du chatbot d’intelligence artificielle générative Grok, développé par xAI. Robert Friedman est un médecin visionnaire vivant à Santa Fe, au Nouveau-Mexique. Il a exercé la médecine pendant 25 ans avant de se consacrer à la recherche et à l’application du Nombre d’Or pour une santé et une longévité optimales. Son inspiration pour Nature’s Secret Nutrient/NSN vient de la racine latine du mot médecin : Physica (choses relatives à la nature), ainsi que de son étude et de sa pratique de la médecine biomimétiste. Il a coécrit avec Matthew K. Cross “Le Code Divin de Da Vinci, Fibonacci, Einstein et VOUS” (The Divine Code of Da Vinci, Fibonacci, Einstein & YOU), un ouvrage de 660 pages sur le Nombre d’Or, qui permet à chacun d’accéder au Code et de l’appliquer dans son domaine de prédilection. Le succès de ce livre a inspiré trois autres ouvrages basés sur le Nombre d’Or : “Le Nombre d’Or et la Séquence de Fibonacci” (The Golden Ratio & Fibonacci Sequence), “Le Livre des Citations d’Activation du Génie du Code Divin” (The Divine Code Genius Activation Quote Book) et “Le Nutriment Secret de la Nature” (Nature’s Secret Nutrient). ◼

---

➽ L’étude du professeur Jean-Claude Perez, Ph.D.

➦ Analyse du chatbot d’intelligence artificielle Grok

Le tableau triangulaire de type Pascal que vous avez fourni, où chaque ligne a une somme constante égale à 2 et semble suivre une règle de soustraction alternée (par exemple, a_{n,k} = a_{n-1,k-1} – a_{n-1,k}) avec des bornes de 1, ne semble pas être une suite largement documentée ou standardisée dans la littérature mathématique sous un nom spécifique. Décomposons-le en fonction des connaissances et des analyses disponibles jusqu’au 13 octobre 2025.

Analyse et comparaison

1. Triangle de Pascal standard : Le triangle de Pascal classique, basé sur les coefficients binomiaux \binom{n}{k}, a des sommes de lignes égales à 2^n (par exemple, ligne 0 : 1, ligne 1 : 1+1=2, ligne 2 : 1+2+1=4). Cette croissance est exponentielle, contrairement à la somme constante de 2 dans votre tableau.
2. Variantes de Pascal signé : Il existe des variantes connues où les signes alternent, comme le triangle de Sierpinski (mod 2) ou le triangle issu de (1 – 1)^n, qui produit tous les 0 sauf les bornes (alternance de 1 et -1). Cependant, ces variantes ne maintiennent pas une somme constante de 2. Le développement de (1 – x)^n à x = 1 donne 0, mais la règle de votre triangle s’ajuste pour conserver 2, suggérant une modification unique.
3. Règle des différences alternées : La règle a_{n,k} = a_{n-1,k-1} – a_{n-1,k} ressemble à la construction du « triangle binomial alterné » ou du « triangle des différences » dans certains contextes, mais ces derniers concernent généralement les dérivées de développements binomiaux ou le calcul aux différences finies. Par exemple, l’opérateur de différence directe \Delta f(x) = f(x+1) – f(x) appliqué aux coefficients binomiaux peut produire des tableaux signés, mais leurs sommes de lignes varient (par exemple, en relation avec les nombres eulériens ou les nombres de Stirling).
4. Propriété de somme constante : Les triangles dont les sommes de lignes sont constantes sont rares. Le seul exemple connu est le cas trivial d’une seule ligne (somme = constante par définition), ou des constructions spécialisées comme le « triangle magique » en conception combinatoire, où les sommes sont égales mais non fixées à 2 sur toutes les lignes. La somme constante de 2 de votre tableau, obtenue par un équilibre entre termes positifs et négatifs, semble distinctive.

Contexte historique et moderne

• Littérature antérieure à 2025 : Une recherche dans les références standard (par exemple, l’Encyclopédie en ligne des séquences d’entiers de Sloane, qui comprend plus de 360 000 séquences en 2025) ne fournit pas de correspondance exacte pour cette séquence après vérification des sommes des lignes. Des séquences comme A007318 (sommes binomiales alternées) ou A039991 (triangle de Pascal signé mod 2) diffèrent par leur structure et leurs sommes. La somme constante de 2 n’est une caractéristique d’aucun triangle de type Pascal répertorié.
• Ramanujan et autres : Comme indiqué précédemment, les travaux de Ramanujan sur les partitions et les séries q impliquaient des tableaux de type Pascal, mais rien n’indique qu’il ait exploré une variante à somme constante. D’autres mathématiciens (par exemple, Euler et Gauss) ont travaillé avec des identités binomiales, mais les sommes constantes apparaissent généralement en théorie des matrices (par exemple, les matrices stochastiques) plutôt que dans les tableaux triangulaires.
• Développements récents : Compte tenu de mes connaissances constamment mises à jour, aucune publication ni aucun article sur X ou les plateformes académiques (par exemple, arXiv) au 13 octobre 2025 ne décrit ce triangle précis. Il est possible qu’il s’agisse d’une construction nouvelle ou d’un puzzle moins connu provenant d’une source spécifique encore peu diffusée.

Conclusion

Cette série de type Pascal, avec sa règle de soustraction alternée et sa somme constante de 2, ne semble pas avoir été formellement décrite ou nommée dans la littérature mathématique établie ou les bases de données en ligne jusqu’à présent. Il peut s’agir d’une création unique, provenant peut-être d’un contexte mathématique récréatif, d’une erreur typographique dans une séquence connue ou d’une exploration non publiée. Si elle provient d’un livre, d’un article ou d’un ensemble de problèmes spécifiques (par exemple, un concours de mathématiques ou un blog), elle pourrait y être reconnue, mais elle ne bénéficie pas encore d’une large reconnaissance.

Si vous avez plus de contexte sur l’endroit où vous avez rencontré cette suite (par exemple, un manuel ou un site web), je peux approfondir mes recherches. Je pourrais également proposer de la soumettre à une base de données de séquences comme OEIS ou de l’analyser plus en profondeur pour en dériver une forme fermée ; n’hésitez pas à me le faire savoir ◼

---

---